|
Determining Distances to Astronomical Objects
The first step for measuring distances to astronomical objects
consists of simple geometrical methods; with them, one can go to a few hundred light years
(but similar methods can be used on larger scales)
For the second step we add photometry and spectroscopy to those geometrical methods.
For even larger distances in the cosmos, one needs additional elements: so-called "standard candles"
For galaxies billions of light years away the cosmological red shift provides an answer. The distance to nearby stars can be determined by their parallaxes. A parallax is the apparent shift of an object as seen from different positions. For example, a finger a few centimeters in front of our nose will shift if we look first with only the left eye and then with the right eye. The explanation is obvious: our eyes aren't in the same place, and hence they have a different angle in order to see the finger. What is important : the difference in the angles depends on the distance; it gets smaller when the distance gets greater. Therefore the difference in angles can be used to measure the distance with simple trigonometry. The distance between our eyes is called the baseline; the bigger the baseline is, the bigger the parallax is, for the same distance of the observed object to the baseline. |
|
Parallax and Star Distances
The stars are very distant from us; therefore we need a much larger baseline then the distance between our eyes. Fortunately we have a rather big baseline available for measuring distances to stars: the diameter of the orbit of the earth (300 million km). Simply look where (at which angle) a star is in the spring in the sky, and then look again where (at which angle) the same star is in the fall in the sky, determine the difference in angles, and we have the parallax for this star - and knowing this and the length of our baseline , we can compute the distance to the star. |
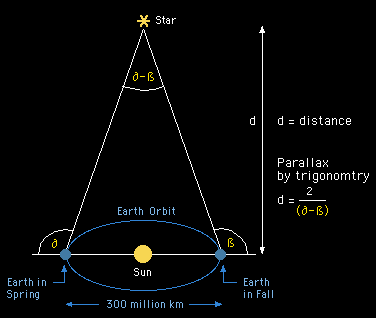
|
|
The first one who was able to measure a parallax of a star was the astronomer Wilhelm Bessel in 1838, at the Observatory
at Koenigsberg. He obtained the value 0.314 arcseconds, which gives a distance of 10 light years.
In the decades since Bessel's measurements, the precision of measurements has increased greatly. Similar geometrical methods can be used for objects which are even billions of light years away (for example, galaxies). In these cases, one has to know the size of an object, then one measures the angles at which one sees the two sides of the object, and from the difference between the angles, one gets the distance. (For methodes to determine the size of a galaxy see the www link at the bottom of this page). |
|
Another method is using the speed of light in the context of a supernova explosion.
A supernova is a massiv star in the latter stages of
stellar evolution that suddenly contracts and then explodes, increasing its
energy output for a brief time as much as a billionfold.
A nice example here is the supernova explosion SN1987A which happened 1987 in the Large Magellanic Cloud, or Galaxy. Before the explosion, the star was already surrounded by a ring of dust. This ring began to glow about a year after the supernova explosion, when the light from the explosion reached it. Hence we know that the diameter of the ring is about two light years, and by measuring its angular diameter in the sky, the distance to the supernova was determined to be approximately 169,000 light years. |
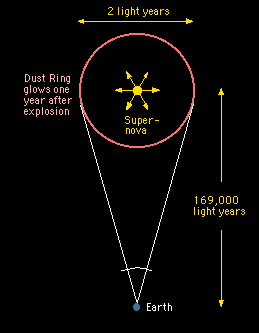
|
|
Section 2 Stellar photometry and spectroscopy For stars so far away that their parallaxes are not measurable (yet), mainly photometry is used, that is, measurements of their brightnesses. We know from physics that brightness decreases proportional to the square of the distance. If we know the brightness of a star and compare this to the measured brightness, we can say how far away the star is. The brightness a star would have in this distance from us is called the absolute brightness of the star. Its actual brightness, which we can observe on earth, is called the apparent brightness. The problem is: How can we know the absolute brightness of a star without knowing its actual distance beforehand? The solution of this problem comes from spectroscopy and an analysis of the spectra of the nearby stars for which we know the distances from their parallaxes. If one looks at the spectrum of a star, one sees dark lines at some wavelengths (some colors) - there is much less light emitted at these wavelengths than at the others. The standard explanation for this is that the atoms in the atmosphere of the star absorb some of the light which is emitted, and each element absorbs only some distinct, characteristic wavelengths of light. If the atoms are excited, they emit these same wavelengths, hence one can determine precisely which spectral lines belong to which element. By looking at the dark lines in the star spectra, we can determine which elements are in its atmosphere. The crucial point is that all stars can be put into groups, so-called spectral classes, where each class has a distinct pattern of dark lines in the spectra, hence a distinct abundance of elements in its atmosphere. These spectral classes are labeled with capital letters: O, B, A, F, G, K, M.
If one examines the stars in the classes further, one sees that each spectral class is associated with a certain color
of the stars, and we know from the theory of radiation that the color depends on the surface temperature of the star
(this is not only true for stars, but in everyday life, too: if one heats up iron, for example, it first glows red, then yellow,
and heating it up even further, it glows white). The temperature is highest for stars in the spectral class O and decreases until the class M.
So, from the color of a star we can deduct the absolute brightness of the star and compare it to its
apparent brightness we see on earth. From the different brightnesses we can then estimate
the distance of the star.
When one determines the distance of an object like a cluster or a galaxy the problem is that one has to know the absolute brightness of the observed object. Fortunately, several types of objects exist for which one can determine their absolute brightnesses without knowing their distances. Such objects are called standard candles.
Cepheids
Hence if one wants to measure the distance of a cluster or a galaxy, one only has to find some Cepheids in it measure their oscillation periods, and use this relationship to determine their absolute brightnesses. By comparing with the apparent brightnesses, one gets their distances. This works for galaxies which are up to a few tens of millions of light-years away.
Supernovae
There is a special type of supernova explosions, the so-called supernovae type I. These can only happen in binary systems: two stars which orbit each other. If they orbit each other closely, one of the stars can draw gases from the other to its surface. A special case now happens if the star which accretes the material from the other star is a white dwarf: if its total mass exceeds a certain limit it starts to collapse. The resulting compression leads to explosive carbon fusion, and the huge amount of energy released thereby disrupts the whole white dwarf. What we observe here is a sudden increase in brightness, followed by a relatively slow decay. This happens because the brightness results mainly from the radioactive decay of nickel and cobalt produced in the explosion (their spectral lines can be observed), and radioactive decay decreases exponentially with time.
What's important now is that there is a universal relationship between the decay rate
of the observed light and the total brightness of the explosion. So by closely observing the light received from such an explosion and
determining the rate at which this light becomes dimmer, one directly gets the absolute brightness of the supernova.
By comparing this with the apparent brightness, one gets the distance of the supernova - and thereby of the galaxy
in which it was situated.
If one closely examines the spectra of far galaxies, one notices that the well-known spectral lines of the elements don't appear at the usual places, but are shifted: they all appear at slightly larger wavelengths than usual. Because "larger wavelength" corresponds to "redder" (red light has the longest wavelength of all visible light), this shift is called the red shift. This red shift was first noticed in 1926 by Hubble. Such shifts are well-known phenomena for sound as well as light: they occur if the object which is emitting the waves is moving with respect to the observer. A red shift implies that they move away from us. An important observation was made by Hubble in 1929 after observing the red shifts of several galaxies: the red shift (and therefore the speed with which they fly away from us) is directly proportional to the distances of the galaxies to us! Hence we see that the farther away a galaxy is, the faster it recedes from us! Nowadays, this is explained using the Big Bang theory, which says that the whole universe expands. Try imagining the universe as the surface of a balloon, with the galaxies firmly attached to its surface. Now if the balloon is inflated, the galaxies obviously move away from each other, and the relative velocity of two galaxies is greater if their relative distance is greater. Hence the method to determine the distance of really distant objects is quite simple: measure its red shift and plug the measured value into a formula provided by the Big Bang theory - this gives the distance. (Although the uncertainties can be up to 20%)
A further complication is that it's not clear what is meant by "distance" here. Often what is reported is not the "real" distance,
which the galaxy has today from us, but the time the light traveled in order to get to us.
Finally, one has to realize that although the methods used to determine distances seem to rely heavily on each other,
there exists instead a whole web of self-correcting and interlocking methods which all come to the same conclusions.
The assumptions which go into the methods are justified by the fact that we get consistent results if we use these assumptions.
|
|
www link : Determining Distances to Astronomical Objects |